Animals (and in extension, humans) are unable to directly perceive the 3D surroundings around us. Each of our eyes projects the 3D world onto 2D, losing the depth dimension. Instead, we rely on our brain to reconstruct these 2D projections to perceive depth. Having more than one eye allows us to geometrically reconstruct depth via triangulation¹, but how are creatures with a single eye (for e.g., due to a defective eye, or due to a birth disorder²) still able to perceive it?

_{^{Each eye of Mantis Shrimp possesses trinocular vision. Cédric Peneau, CC BY-SA 4.0, via Wikimedia Commons}}

We rely on monocular cues for perceiving 3D even with a single eye. These monocular cues include those from the static image such as perspective, relative sizes of familiar objects, shading, occlusion, etc.; and those from motion, such as parallax, depth from motion, etc.³

Can we teach machines to estimate depth from a single image?

If animals are able to use these cues to reason about the relative 3D structure, the question arises, is there a way to make machines do the same? A famous paper from 2009 called Make3D⁴ says “yes!”.

But this post is not about that. We will be looking at more recent neural network based approaches. After all, neural networks can be thought as function approximators and with enough data, should be able to approximate the function $\mathcal{f}$ that maps an RGB pixel $i \in \mathbb{R}^3$ to its depth $d$

$d = \mathcal{f}(i)$

In-fact we are looking at methods that do not rely on the availability ground-truth (GT) depths. Why? Because it is expensive and tedious to gather such ground truth and difficult to calibrate and align different sensor ouputs, making it difficult to scale. But, how can we teach a neural network to estimate the underlying depth without having ground truth? Thanks for asking that! Geometry comes to the rescue. The idea is to synthesize different views of the same scene and compare these synthesized views with the real ones for supervision. It underlies on the brightness constantcy assumption⁵, where parts of the same scene are assumed to be observed in multiple views. A similar assumption is used in binocular vision, where the content of what a left eye/camera sees is very similar to that of what the right one sees; and in motion/optical-flow estimation, where the motion is the vector $u_{xy}, v_{xy}$ defined by the change in pixel locations as

$I(x, y, t) = I(x + u_{xy}, y + v_{xy}, t + 1)$

Stereo supervision

Garg et.al., propose a method called monodepth⁶, to estimate depth from a single image, trained on stereo image pairs (without the need for depth GT). The idea is similar: synthesize the right view from the left one and compare the synthesized and the real right views as supervision.

_{^{Left and right images of the same scene from the KITTI dataset⁷}}

But, how will this help learn depth? This is because view synthesis is a function of depth. In a rectified stereo setting, the optical flow is unidirectional (horizontal) and so only its magnitude a.k.a. disparity is to be found. The problem then boils down to finding a per-pixel disparity that when applied to the left image, gives the right image.

$I_{l}(x, y) \stackrel{!}{=} I_r(x + d_{xy}, y)$

The depth from disparity can be calculated by $\text{depth} = \frac{\text{focal length}\times\text{baseline}}{\text{disparity}}$.

triangulation

_{^{Depth as a function of disparity via triangulation¹. By fr:Utilisateur:COLETTE, CC BY-SA 3.0, via Wikimedia Commons}}

The pipeline goes as follows:

A network predicts the dense disparity map of the left image.
Relative camera pose (Ego-motion) is known, which in this case of recitfied stereo is just a scalar, representing the horizontal shift of 5.4 cm in X-direction.
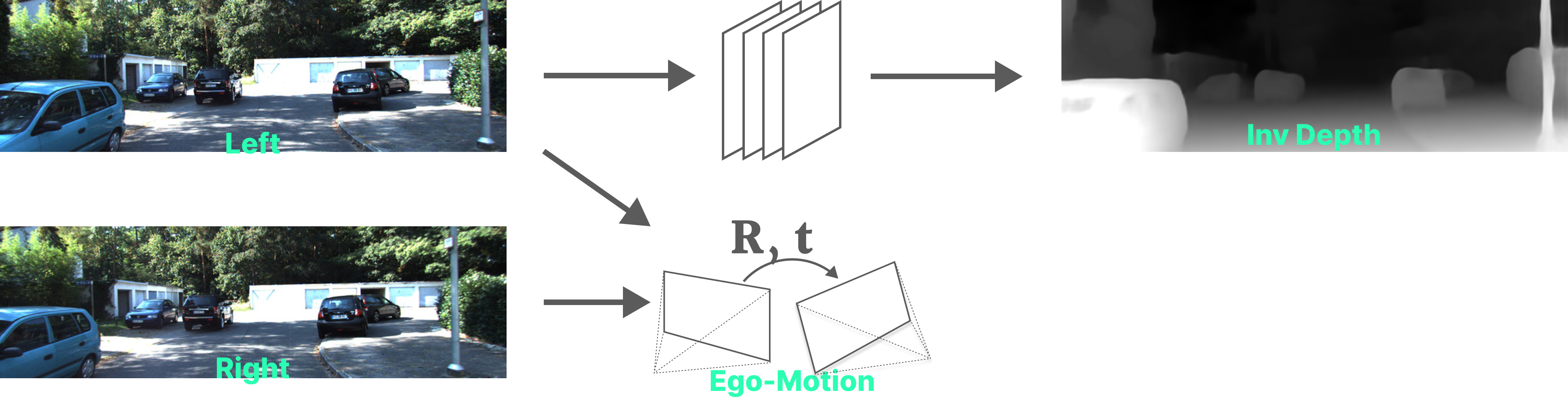
Using the estimated disparity, a per-pixel flow in the left image’s coordinates is calculated based on the known relative rigid camera pose.
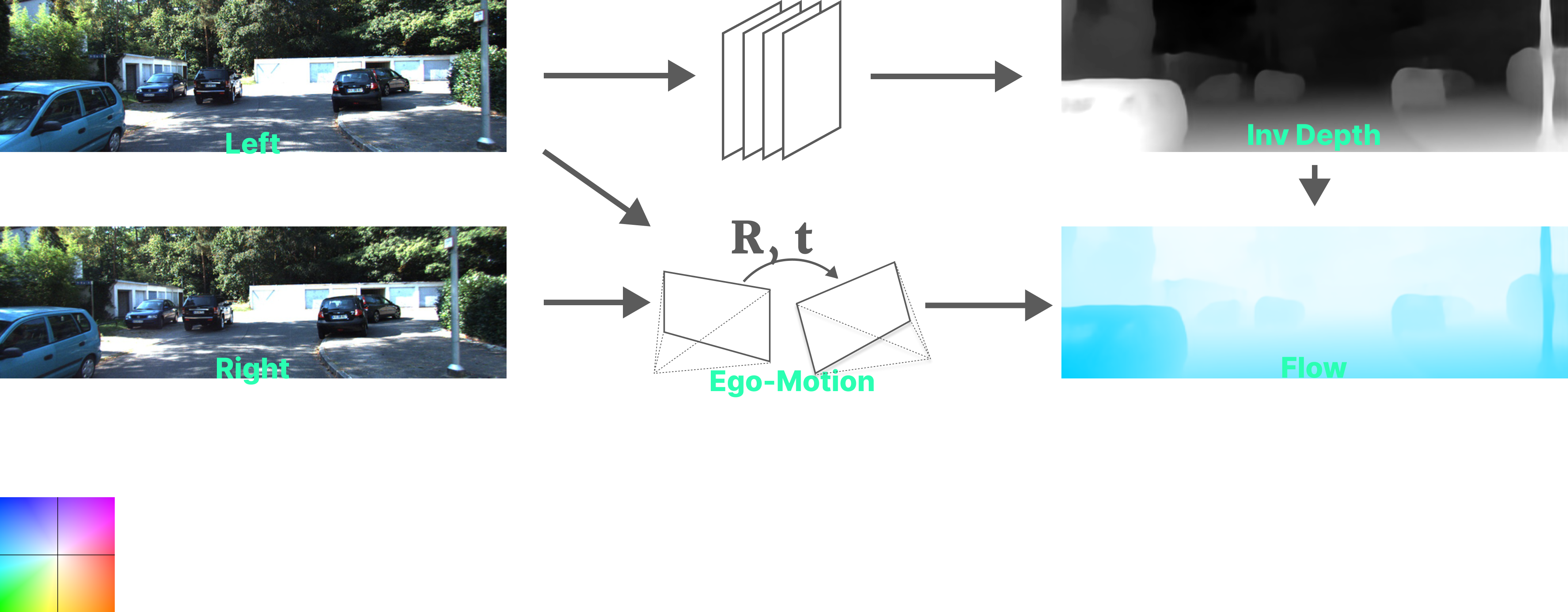
The right input image is warped using the flow, into the view of the left image.
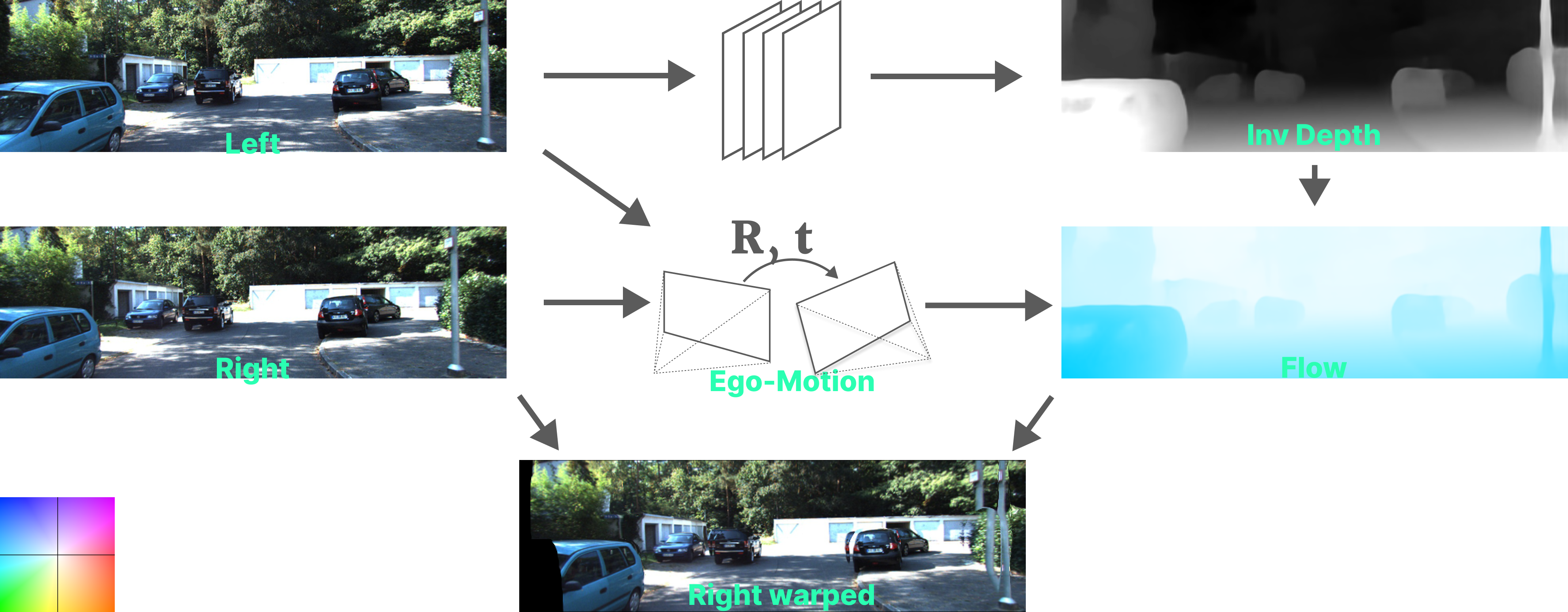
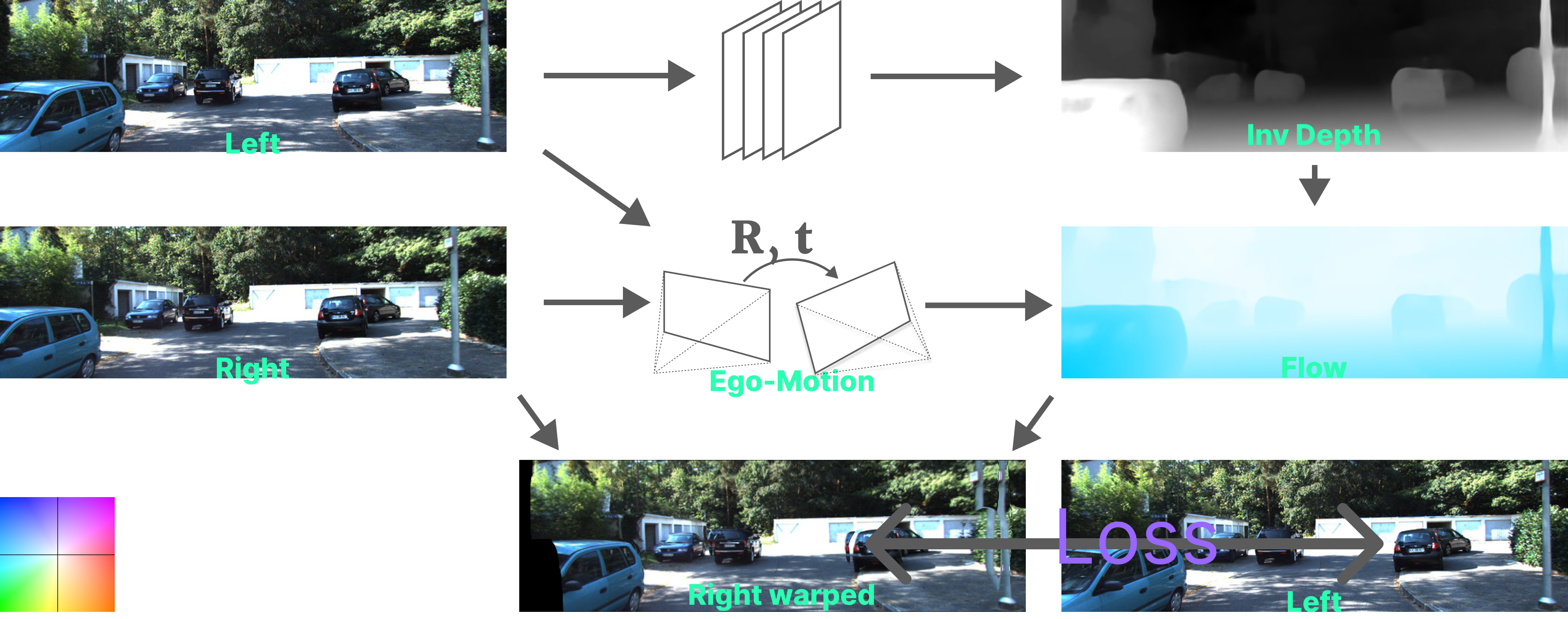
The warped right image onto the left’s view needs to be consistent with the original left image if the estimated depth from the network is correct. A loss is thus calculated between the two and is propogated through the depth network, thereby, making it learn to predict monocular depth.

The Monocular case

While the stereo case is analogous to animals using binocular vision to perceive 3D, what about the monocular case, where creatures are still able to reconstruct the underlying 3D structure of the scene using a single eye? Can the above method be extended for monocular case?

_{^{Cyclops by Nilesdino, CC BY-NC-ND 3.0}}

The answer is not straightforward. Even if we think about exploiting motion, the relative ego-motion of the camera from one frame at time $t$ to the next $t+1$ is not known, unlike in stereo case where the pose between the left and right cameras is known (and uni-directional for calibrated cases). Not only is the camera pose not known between two timesteps, it is also changing and not constant as in stereo case. So, in order to extend the stereo approach to monocular case, relative camera pose or camera ego-motion has to also be predicted between any 2 consecutive frames.

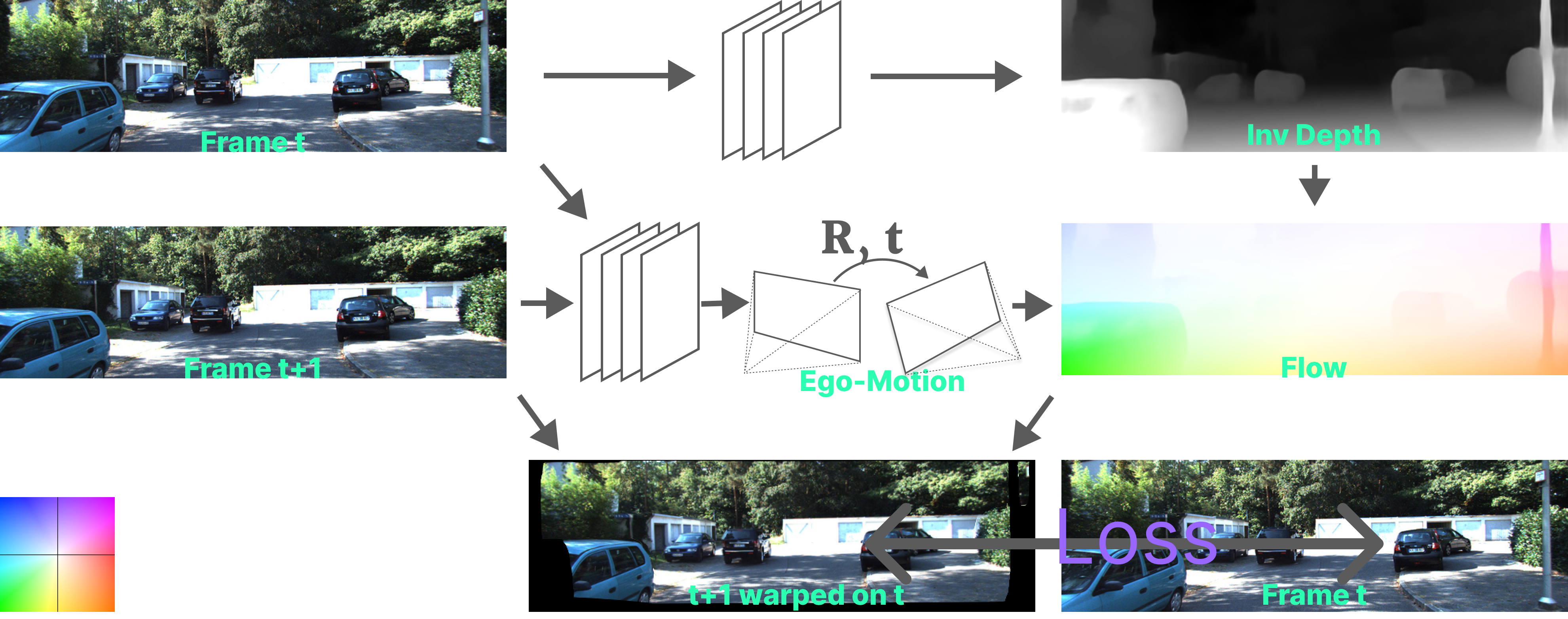
_{^{SfMLearner: Unsupervised Learning of Depth and Ego-Motion from Video⁸}}

Zhou et.al’s SfMLearner: Unsupervised Learning of Depth and Ego-Motion from Video⁸ does exactly that. They introduce an additional network which estimates the 6 DOF rigid ego-motion/pose $T \in \text{SE}(3)$, between the cameras of the two consecutive frames with pixel locations $[x_t, y_t, 1]^T$ and $[x_{t+1}, y_{t+1}, 1]^T$ resp.. The working principle is similar to before but the warping of one frame onto the other is done by

$\left(\begin{array}{c}x_{t+1} \\ y_{t+1} \\ 1 \end{array} \right) \stackrel{!}{=} KTK^{-1}d_{xy} \left(\begin{array}{c}x_t \\ y_t \\ 1 \end{array} \right)$,

where the camera intrinsics matrix $K = \Bigl[\begin{smallmatrix}k_x&0&p_x \\ 0&k_y&p_y \\ 0&0&1\end{smallmatrix} \Bigr]$, with focal lengths $f_x, f_y$ and principal point $p_x, p_y$ is assumed to be known. Next, we will see how this makes sense

$K^{-1}d_{xy} \left(\begin{array}{c}x_t \\ y_t \\ 1 \end{array} \right)$

Intiutively, given the depth $D$, one could unproject the image coordinates using the depth and the inverse camera intrinsics onto 3D.

$TK^{-1}d_{xy} \left(\begin{array}{c}x_t \\ y_t \\ 1 \end{array} \right)$

Then, the camera is transformed to that at time $t+1$.

$TK^{-1}d_{xy} \left(\begin{array}{c}x_t \\ y_t \\ 1 \end{array} \right)$

And, the points are projected back onto this transformed camera using the same camera intrinsics, to synthesize the image at time $t+1$

$I_{t} \, \Big\langle KTK^{-1}d_{xy} \left(\begin{array}{c}x_t \\ y_t \\ 1 \end{array} \right) \Big\rangle $

, where $\Big\langle \Big\rangle $ is the sampling operator. This projection of $I_t$ onto the coordinate at time $t+1$ geometrically synthesizes the image $\hat{I}_{t+1}$ and can now be compared to the original frame from time $t+1$ and the loss is backpropogated to both the depth and the pose networks.

Note

This is not exactly correct. The pose $T$ is used, not to transform the camera, but to transform the point cloud (in the reverse direction to that of the camera pose), and the image $I_{t+1}$ is warped onto $t$, but the underlying concept remains the same. I will now explain how this idea is executed.

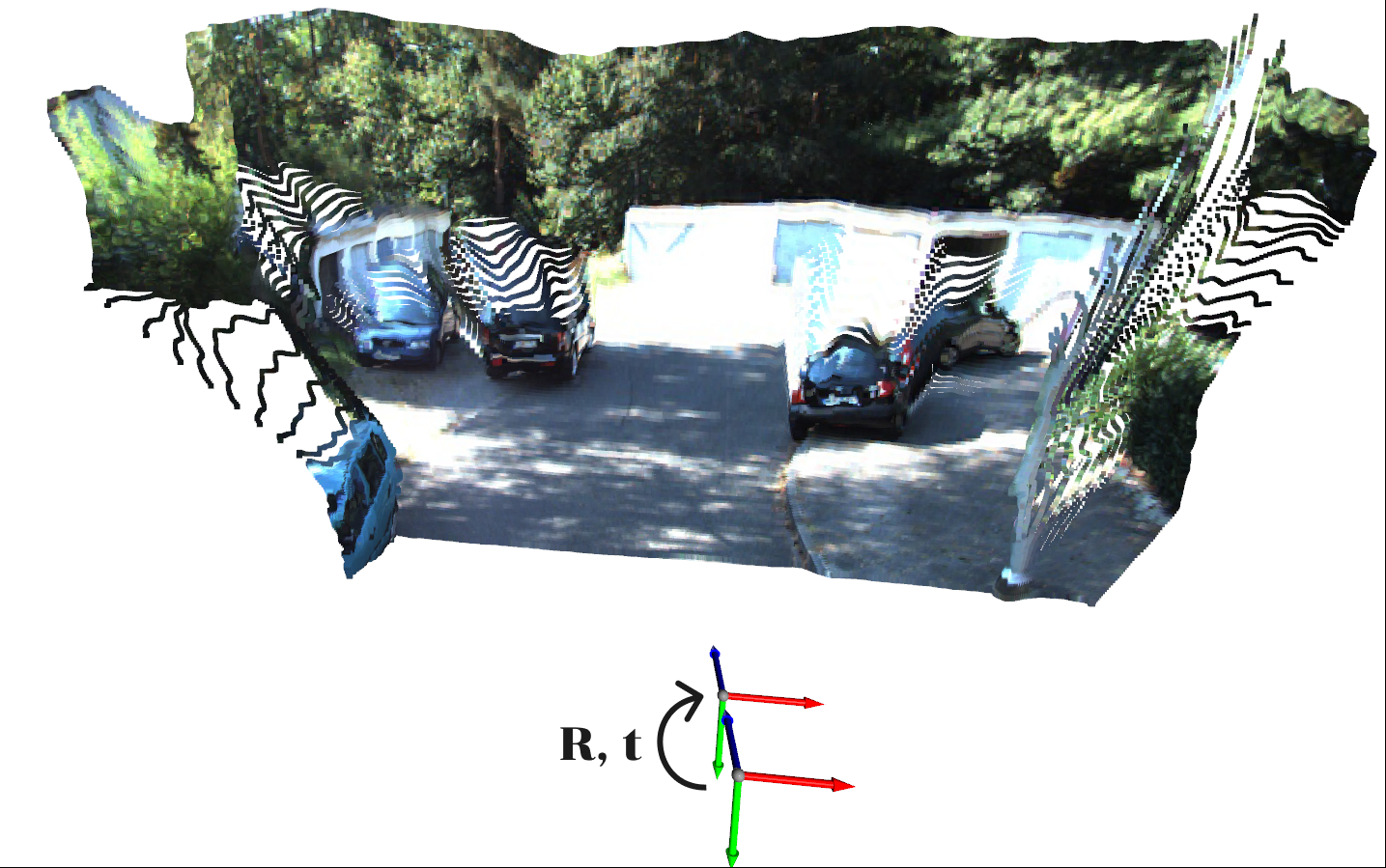
Flow field due to rigid camera motion

The resulting 2D rigid flow (flow due to rigid camera motion) that transforms each pixel at time $t+1$ to that at time $t$ can be visualized as follows.

$KTK^{-1}d_{xy} \left(\begin{array}{c}x_t \\ y_t \\ 1 \end{array} \right)$

Note that this flow is a function of depth and 6 DOF transformation, i.e. the rigif flow field depends not only on the rigid 6 DOF transformation of the camera, but also on the distance of each point to the camera. Intuitively, this makes sense since objects fat away seem to move less in the image plane than those far away. This is known as motion parallax

_{^{Motion Parallax: Objects farther away appear to move lesser than those close-by. Nathaniel Domek, CC BY 3.0, via Wikimedia Commons}}

If this article was helpful to you, consider citing

@misc{suri_how_monocular_depth_estimation_2022,
      title={Self-supervised monocular depth estimation},
      url={https://zshn25.github.io/How-Monocular-Depth-Estimation-works/}, 
      journal={Curiosity}, 
      author={Suri, Zeeshan Khan}, 
      year={2022}, 
      month={Oct}}

References:

Triangulation ↩ ↩²
Cyclopia ↩
Monocular cues for depth perception ↩
A. Saxena, M. Sun and A. Y. Ng, “Make3D: Learning 3D Scene Structure from a Single Still Image,” in IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 31, no. 5, pp. 824-840, May 2009, doi: 10.1109/TPAMI.2008.132. ↩
Brightness Constancy ↩
Garg, R., B.G., V.K., Carneiro, G., Reid, I. (2016). Unsupervised CNN for Single View Depth Estimation: Geometry to the Rescue. In: Leibe, B., Matas, J., Sebe, N., Welling, M. (eds) Computer Vision – ECCV 2016. ECCV 2016. Lecture Notes in Computer Science(), vol 9912. Springer, Cham. ↩
A Geiger, P Lenz, C Stiller, and R Urtasun. 2013. Vision meets robotics: The KITTI dataset. Int. J. Rob. Res. 32, 11 (September 2013), 1231–1237. https://doi.org/10.1177/0278364913491297 ↩
T. Zhou, M. Brown, N. Snavely and D. G. Lowe, “Unsupervised Learning of Depth and Ego-Motion from Video,” 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 2017, pp. 6612-6619, doi: 10.1109/CVPR.2017.700. ↩ ↩²