Discrete convolutions are characterized as matrix multiplications and are thus able to execute really fast on GPUs. But, how are they characterized as matrix multiplications? Are convolutions linear? Let’s find out.

1. Definitions:

1.1 Convolution

Let $f,g$ be two real valued functions in 1D $f,g : \mathbb{R}\to \mathbb{R} $, the convolution of $f$ with $g$ is defined as

$f * g = \displaystyle\int_{\mathbb{R}} \! f(t) g(x-t) \, \mathrm{d}t$

An example of the 1D convolution of a box function with itself can be seen in the example below

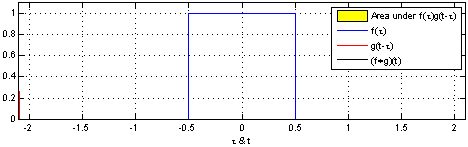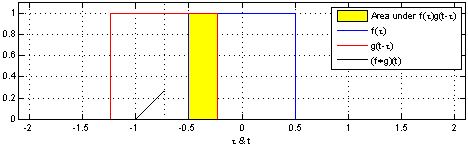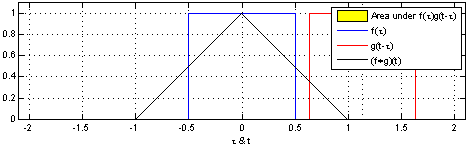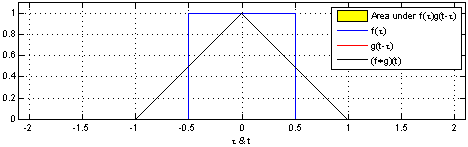convolution Convolution of a box function with itself. By Brian Amberg derivative work: Tinos, CC BY-SA 3.0.

1.2 Linearity

Let $K$ be a mapping $K : A \to B $ of two vector spaces $A,B$. Such a mapping is linear if

$K(\alpha x+\beta y) = \alpha K(x)+ \beta K(y) $

for all $ x \in A, y \in B$ and scalars $\alpha ,\beta \in \mathbb{R}$.

In simple words, a linear mapping/transformation preserves vector addition and scalar multiplication. It doesn’t matter whether the linear mapping is applied before or after vector addition and scalar multiplication.

2. Linearity of Convolution

To show that convolution is linear, for $ \ x,y,f : \mathbb{R}\to \mathbb{R}, \ \alpha ,\beta \in \mathbb{R}$, we need to prove

$(\alpha x + \beta y) * f \stackrel{!}{=} \alpha (x * f) + \beta (y * f)$

2.1 Proof

(αx+βy)∗f=∫R ⁣(αx(t)+βy(t))f(x−t) dt=∫R ⁣(αx(t)f(x−t)+βy(t)f(x−t)) dt=α∫R ⁣x(t)f(x−t) dt+β∫R ⁣y(t)f(x−t) dt(Linearity of integral)=α(x∗f)+β(y∗f)\large{\begin{aligned} (\alpha x + \beta y) * f &= \int_{\mathbb{R}} \! (\alpha x(t) + \beta y(t)) f(x-t) \, \mathrm{d}t \\ &= \int_{\mathbb{R}} \! (\alpha x(t)f(x-t) + \beta y(t)f(x-t)) \, \mathrm{d}t \\ &= \alpha \int_{\mathbb{R}} \! x(t)f(x-t) \, \mathrm{d}t + \beta \int_{\mathbb{R}} \! y(t)f(x-t) \, \mathrm{d}t \quad \text{(Linearity of integral)}\\ &= \alpha( x * f) + \beta( y * f)\end{aligned} }

proves that convolution is a linear operator. This proof directly follows from that fact that an integral is a linear mapping of real-valued (integrable) functions to $\mathbb{R}$.

$\small{\displaystyle\int_a^b{[{c_1}{f_1}(x)+{c_2}{f_2}(x)+\cdots +{c_n}{f_n}(x)]dx}={c_1}\displaystyle\int_a^b{f_1(x)dx}+{c_2}\displaystyle\int_a^b{f_2(x)dx}+\cdots +{c_n}\displaystyle\int_a^b{f_n(x)dx}}$

3. Discrete convolution as matrix multiplication

So, if convolutions are linear, we should be able to express the discrete convolution as a matrix multiplication. In fact, one of the input function is converted to a Toeplitz matrix, enabling a discrete convolution to be characterized by a convolution.

y=h∗x=[h10⋯00h2h1⋮⋮h3h2⋯00⋮h3⋯h10hm−1⋮⋱h2h1hmhm−1⋮h20hm⋱hm−2⋮00⋯hm−1hm−2⋮⋮hmhm−1000⋯hm][x1x2x3⋮xn]y = h \ast x = \begin{bmatrix} h_1 & 0 & \cdots & 0 & 0 \\ h_2 & h_1 & & \vdots & \vdots \\ h_3 & h_2 & \cdots & 0 & 0 \\ \vdots & h_3 & \cdots & h_1 & 0 \\ h_{m-1} & \vdots & \ddots & h_2 & h_1 \\ h_m & h_{m-1} & & \vdots & h_2 \\ 0 & h_m & \ddots & h_{m-2} & \vdots \\ 0 & 0 & \cdots & h_{m-1} & h_{m-2} \\ \vdots & \vdots & & h_m & h_{m-1} \\ 0 & 0 & 0 & \cdots & h_m \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \\ x_3 \\ \vdots \\ x_n \end{bmatrix}

– Discrete convoliton using Toeplitz matrix

If this article was helpful to you, consider citing

@misc{suri_is-convolution-linear_2021,
      title={Is convolution linear?},
      url={https://zshn25.github.io/is-convolution-linear/}, 
      journal={Curiosity}, 
      author={Suri, Zeeshan Khan}, 
      year={2021}, 
      month={Mar}}